PyOrbit Contributions

Mentioned previously, PyOrbit is a simulation framework used to better study particle accelerators. The framework uses two major simulation tools; a bunch and nodes. A bunch is a collection of marco-particles, which can have a variety of attributes and flags. Nodes are used at the segmentation tool, in which a collection of nodes can be used to create a complete lattice. A defined lattice keeps the order of all nodes, and simulates an accelerator.

Uniform Focusing

My project was to implement a Uniform Focusing Lattice to help study self-consistent beams. Self-consistent beams are defined as a particle distribution that has a consistent form and density through all linear transformations and linear forces due to spacecharge.

A major concept in the field of beam physics is linear transformations (i.e. FODO matrices), specifically in 6D phase space. The linear transformations of the 6 coordinates can be represented by the transport matrix $R(s,s_0)$, where the it is a function of the points $s$ and $s_0$.

\[Phi(s) = R(s,s_0) \cdot \Phi(s_0)\]

For the concept of uniform focusing our transport matrix simplifies because we make simple assumptions about the symmetries and it is defined in terms of the Twiss parameters.

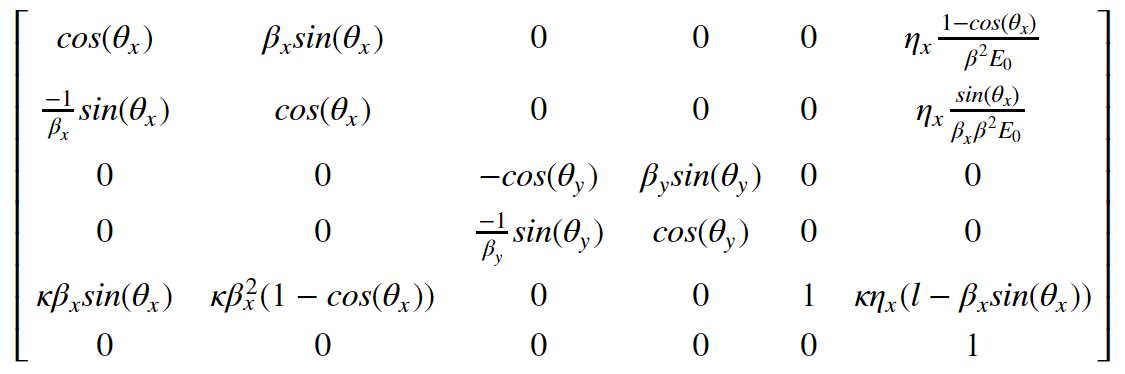
Using this transport matrix and parameters defined in by the particle distribution. We created a new node class that can be given certain parameters like element length, curvature, and XY tunes to determine the values to fill the matrix. We determined the validity of the model using a test case of the following specifications:

• 200 Nodes - 10 loops (2000 eff. passes)
• 50 meter length lattice - LINAC
• XY Tunes = \(2 \pi\)
• Including Spacecharge

From the test case we were looking for two major concepts to be upheld from the model, matching initial and final distributions and a decrease in the oscillation frequency from the statistical beta function.

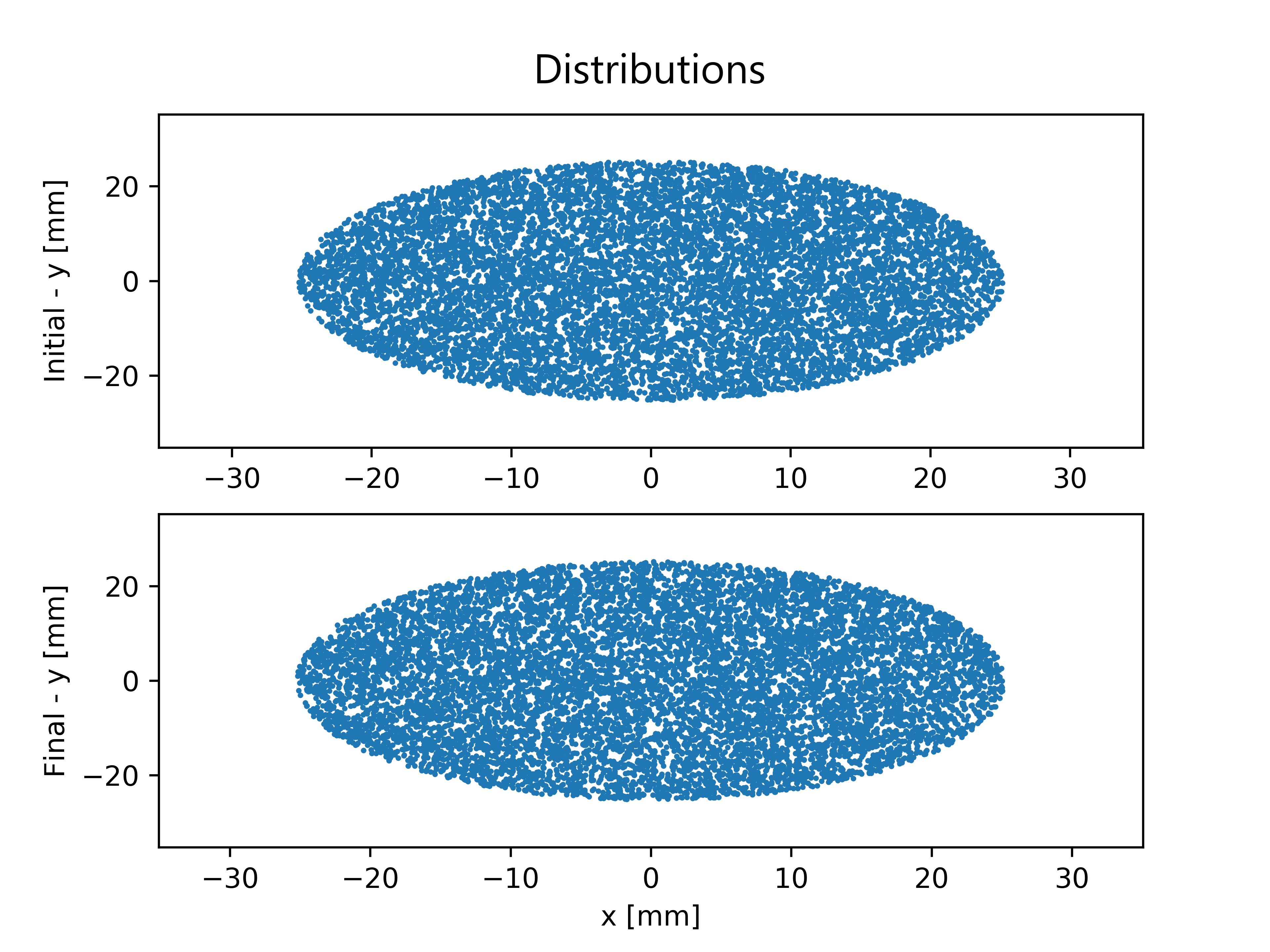
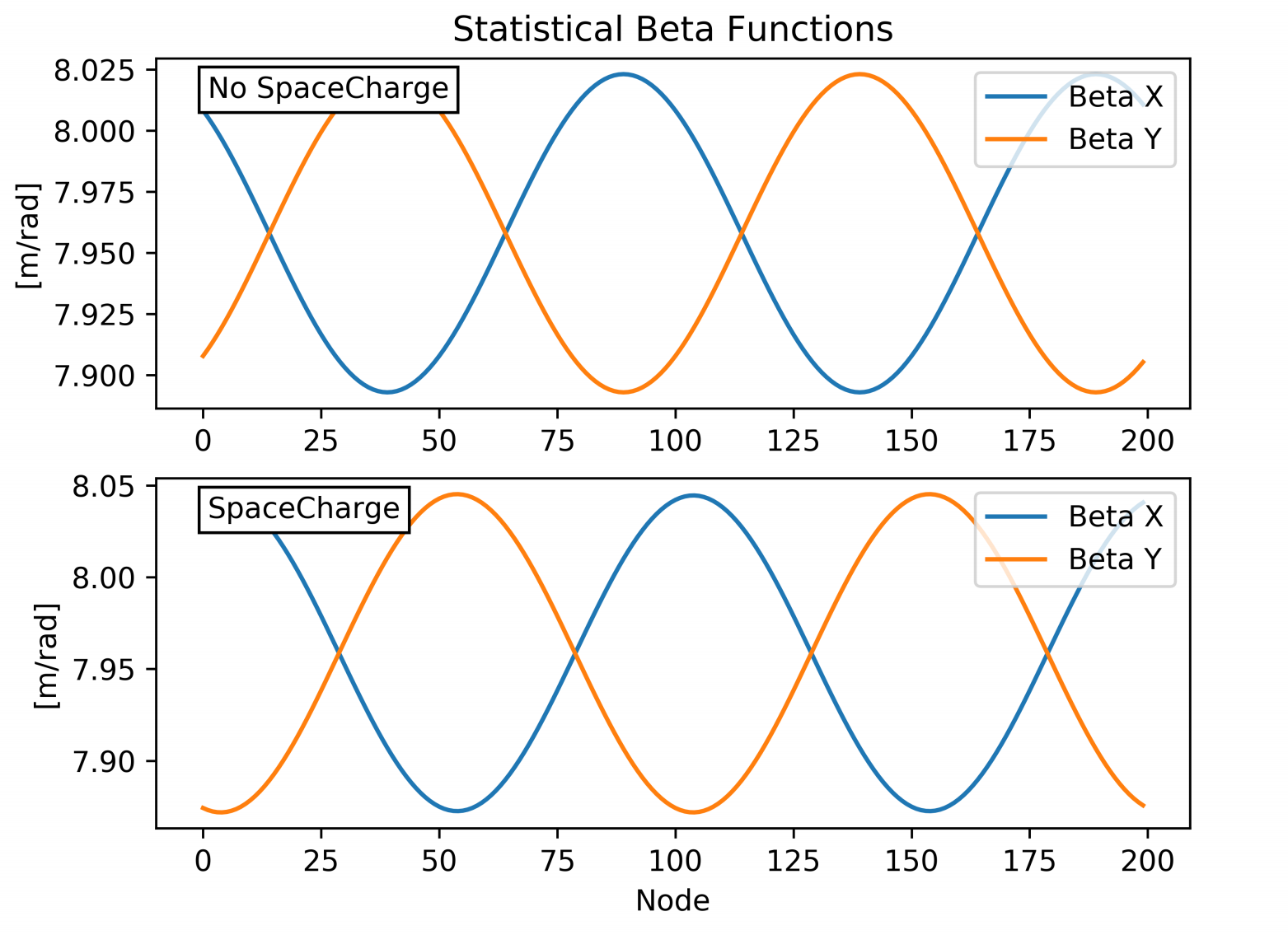
As seen from the results, both criteria for our model were met. Fortunately, we had about 7 weeks left for the internship and were able to continue the project to create 2 envelope solvers.

Envelope Solver

The major assumptions for the solver are a periodic lattice and self-consistent beam. Including spacecharge forces, we have a modified Hill equation given by,

\[x'' + k_x(s) x - \frac{2\Lambda}{a(s)(a(s)+b(s))} x = 0\] \[y'' + k_y(s) y - \frac{2\Lambda}{b(s)(a(s)+b(s))} y = 0\]

Therefore our envelope solver was based on Eqs. (2-3) where $u$ and $\nu$ represent the envelope in the X and Y cross section of the beam, respectively.

\[u'' + k(s) u = \frac{E_u^2}{u^3} + \frac{2 \Lambda}{\sqrt{u^2 + 4 D^2\sigma_E^2} + \nu}\]

We made a new child node class to implement the envelope solver, which could be inserted into each node in a lattice. The solver will only use a single particle bunch, which will hold the envelope initial parameters defined by the Twiss parameters. Testing the envelope solver, we used the same test case defined above (50m, 200 Nodes), and created two different bunches. The first bunch was a collection of 10,000 macro particles, and the second contained only an envelope particle. Comparing the simulation results from the two bunches we determined the solver works as intended.

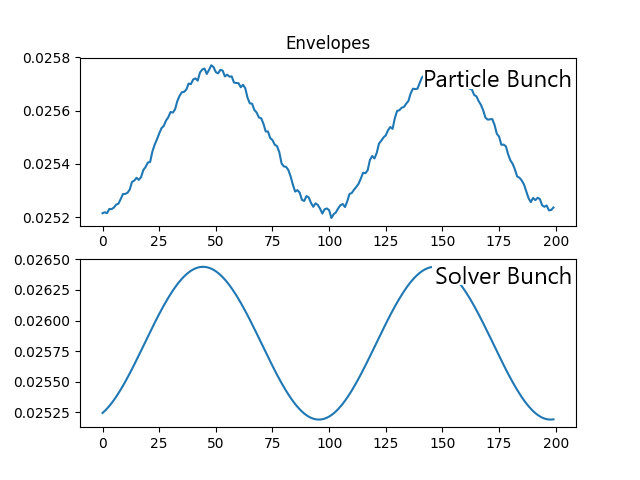
Tilting Envelope Solver

Moving forward in the project, we aimed to make a different solver that could add a wider range of distributions/beams that can use the envelope solver. This final envelope solver was made to handle tilting beams in contrast to basic rotating beams seen in the figures above. Unfortunately, the tilting envelope solver was tested using a particle bunch. However, we did do basic examples to verify it worked.

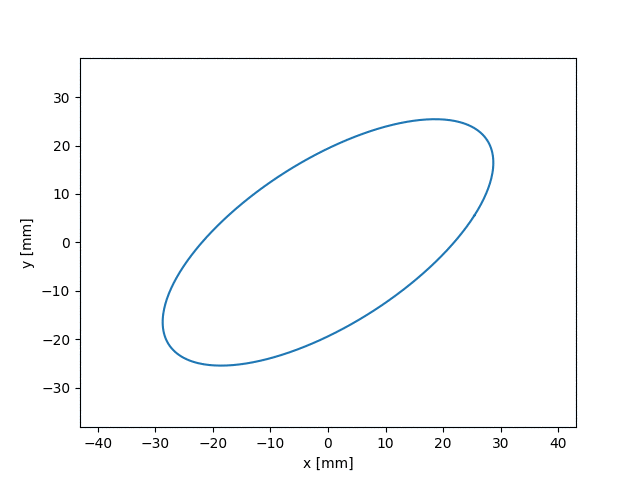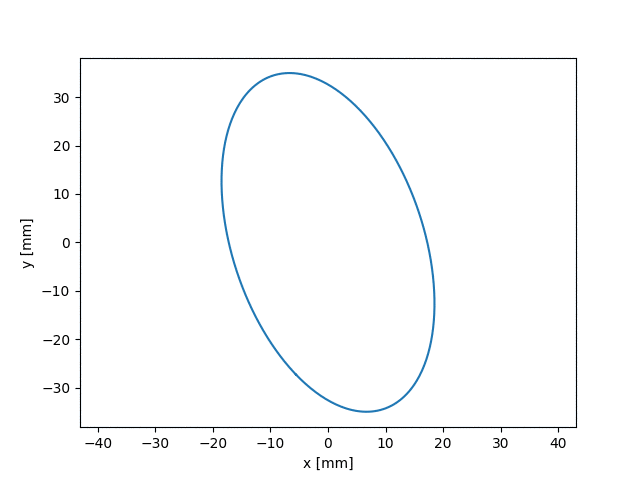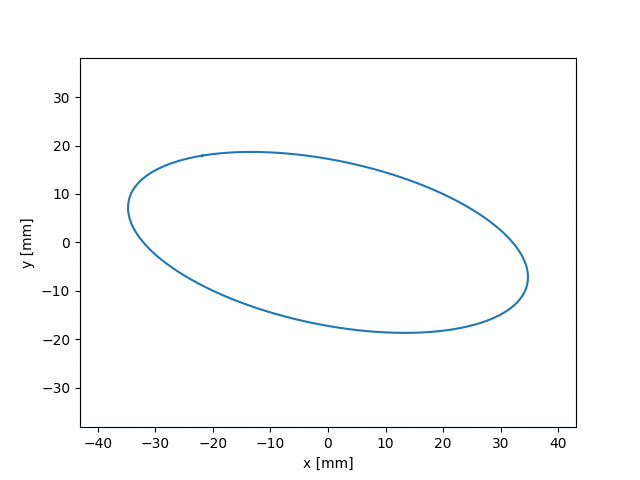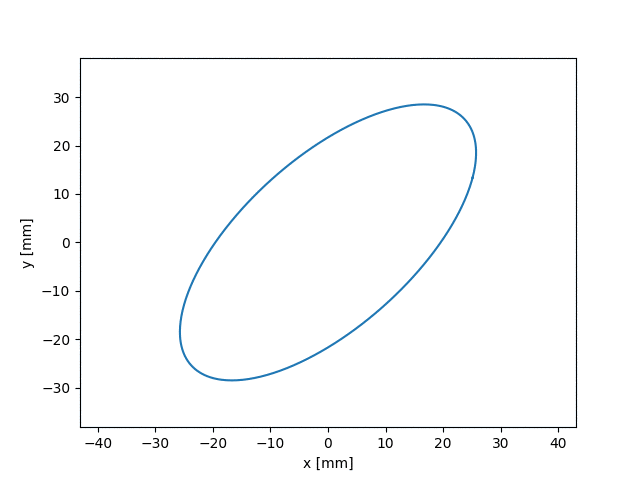
These solvers and Uniform Focusing model will help study the behavior of self-consistent beams. Such beams may be able to provide low-loss environments. For high intensity accelerators this may lead to increased longevity, reduced costs, and higher power. If the project was continued, the major simulations and experimental runs would have involved self-consistent beams with extraneous particles.

This would allow for a significant decrease in computational power and processing time. Using the envelope solver would give details about the beam and spacecharge forces that would effect the external particles.

References and Sources

The contributions made for PyOrbit can be found at the PyOrbit forked repository on my GitHub.

• Rosenzweig, James B. Fundamentals of Beam Physics. Los Angeles, University of California, 2012.
• Edwards, D.A. and M.J.Syphers. An Introduction to the Physics of High Energy Accelerators. Wiley-VCH, 1993.